지난번에 Disctrete RV에서 Binomial과 Poisson 분포에 관해 다뤘다면
이번에는 Continuous RV에서 Exponential RV을 알아보자.
What is
Exponential Random Varialbe
Exponential RV란 한글로 지수분포라고 한다.
사건이 독립적일때, 일정 시간동안 발생하는 사건의 횟수가 포아송 분포를 따르면,
다음 사건이 일어날 때까지 대기시간은 Exponential 분포를 따른다.
즉, 시간에따른 함수이기 때문에 continuous한 형태임을 알 수 있다.
이 분포의 PDF는 이름에서 알 수 있듯이 지수함수적으로 감소하게 되며
CDF는 각각의 PDF를 적분한 형태이기 때문에 증가하는 모양을 보인다.
PDF는 다음과 같다.
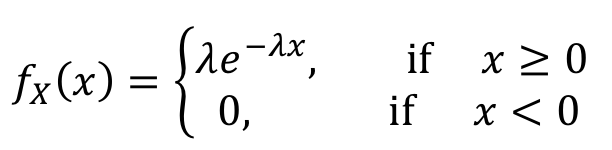
이제 매트랩을 이용해 PDF로 CDF를 구하고 그래프를 그려보자.
Using MATLAB
바로 매트랩으로 실현을 하기에는 다소 무리가 있다.
우선 Exponential RV는 시간에 대한 함수이므로 x축은 시간을 의미한다. 즉, 무수히 많은 x값을 표현해야 하는데
매트랩은 컴퓨터로 무한대의 값을 표현할 수 없기 때문에 Inverse Transformation Method를 이용해야한다.
쉽게말해 역함수를 통해 해결할 수 있다.
이를 해결하기 위한 접근방법은 다음과 같다.
1. 0부터 10까지 100개의 index를 형성해준다.
2. 0부터 1까지 random한 y값을 10만개 생성한 후에 각각의 값을 count해서 x축에 대입해준다.(이를 앞으로 bin이라고 부르자.)
3. exponential RV의 PDF수식을 inverse 해준다.
4. PDF를 구하는 방법은 ( (bin의 count수 / 전체생성smaple수) / (bin의 범위 / bin의 길이) )로 계산할 수 있다.
5. CDF는 PDF의 누적합(적분처럼)을 통해 구할 수 있다.
<code>
# Define U = rand(1,100000); x_range=linspace(0,10,100); x_index = linspace(0,10,99); X = -log(1-U); N = histcounts(X,x_range); # Exponential RV PDF Empirical_PDF = (N/length(U))/(x_range(end)/length(x_range)); # 경험적 Theoretical_PDF = 1*exp(-1*x_range); # 이론적 # Exponential RV CDF Empirical_CDF =cumsum(Empirical_PDF)*(x_range(end)/length(x_range)); Theoretical_CDF = -(exp(-1*x_range)-1); # Plot subplot(2,1,1) bar(x_index,Empirical_PDF) grid on hold on plot(x_range,Theoretical_PDF,'LineWidth',2) xlabel("x"), ylabel("PDF"), legend("Empirical PDF", "Theoretical PDF") subplot(2,1,2) bar(x_index,Empirical_CDF) grid on hold on plot(x_range,Theoretical_CDF,'LineWidth',2) xlabel("x"), ylabel("CDF"), legend("Empirical CDF", "Theoretical CDF")<result>
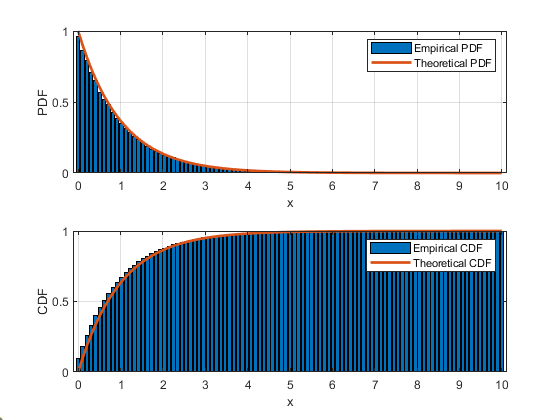
실제로 이론적인 수식과 random한 수를 생성해서 출력한 것과 근사함을 알 수 있다.
'테크 > MATLAB' 카테고리의 다른 글
| [MATLAB] 이산확률변수(Discrete Random Variable) (0) | 2021.10.31 |
|---|---|
| [MATLAB] 이미지 프로세싱(R, G, B 이진화) (0) | 2021.07.13 |
| [MATLAB] 신호의 주파수 해석(Fourier Analysis in Frequency Domain) (0) | 2021.07.10 |
| [MATLAB] 악보 만들고 연주하기 & 파형분석 (0) | 2021.07.10 |
| [MATLAB] 이미지 분석 & 히스토그램(RGB histogram) (0) | 2021.07.09 |
