확률과 통계학 수업을 하면서 여러 확률모델에 관해 배웠다. 그중 이산적(discrete)인 Empirical PMF을 통해 Binomial RV와 Poisson RV를 비교해 보자.
What is
Binomial Random Variable?
Binomial RV란 고등학교 확률과 통계 수업에서 배우는 '이항분포'와 같은 개념이다.
n번의 독립시행중 성공할 확률이 p일 때 갖는 이산확률분포이다.
말로 표현하기에는 와닿지 않으니 바로 PMF를 확인해 보자
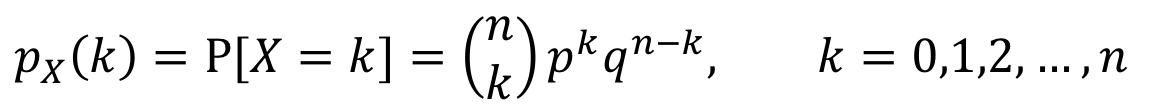
위 식을 해석하자면
총 n번 시행 중
성공할 확률 : p, 실패할 확률 : q (=1-p)
일때 성공을 k번, 실패를 n-k번 발생할 때의 확률을 표현한 식이다.
평균 : E[X] = np
분산 : VAR[X] = npq = np(1-p)
Binomial RV는 매우 general한 형태이다.
n=1이면 Bernoulli(베르누이) RV를 형성하며
n이 많고, p가 적으면 Poisson(포아송) RV를 따른다.
Poisson RV의 PMF는 다음과 같이 표현되는데 과연 Binomial RV로부터 Poisson RV를 도출할 수 있는지 매트랩으로 확인해 보자.
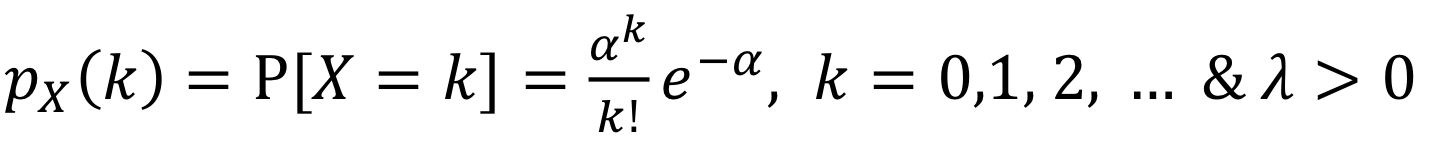
Binomial RV
VS
Poisson RV
앞서 Binomial RV에서 n이 많고 p가 적으면 Poisson RV를 따른다고 했다.
그렇다면 두개의 테스트를 통해
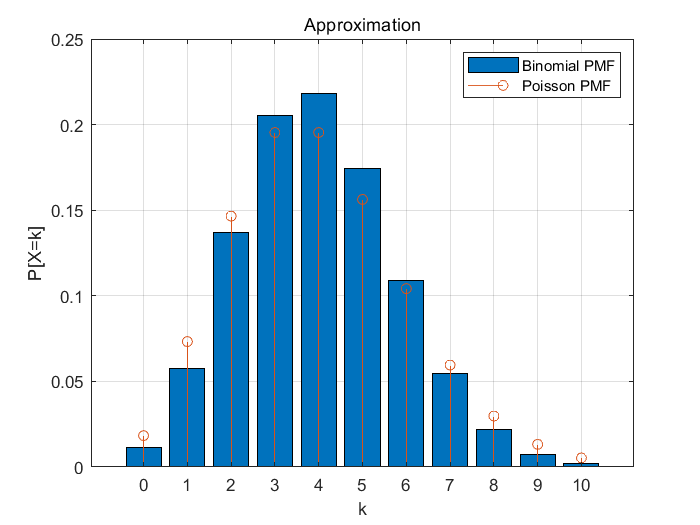
i) n=20, p=0.2
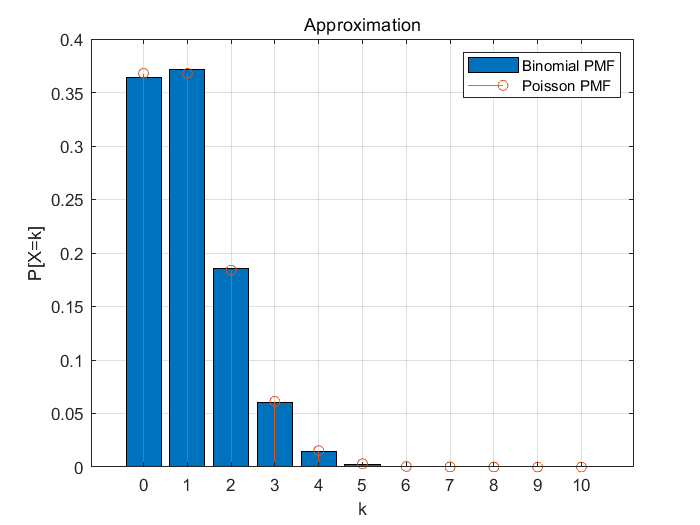
ii) n=50, p=0.02
일때 그래프를 비교해 보자.
n=20, p=0.02 일때
<code>
n=20; #시행횟수
p=0.2; #확률
a = n*p;
x = linspace(0,10,11); #0부터 10까지 11개의 인덱스 생성
Binomial_PMF = linspace(0,10,10);
Poisson_PMF = linspace(0,10,10);
for k = 0:10
Binomial_PMF(k+1) = nchoosek(n,k)*p^k*(1-p)^(n-k);
Poisson_PMF(k+1) = ((a^k)/factorial(k))*exp(-a);
end
bar(x,Binomial_PMF())
hold on
grid on
stem(x,Poisson_PMF)
xlabel("k")
ylabel("P[X=k]")
title("Approximation")
legend("Binomial PMF", "Poisson PMF")<result>
n=50, p=0.02일때
<code>
n=50;
p=0.02;
a = n*p;
x = linspace(0,10,11);
Binomial_PMF = linspace(0,10,10);
Poisson_PMF = linspace(0,10,10);
for k = 0:10
Binomial_PMF(k+1) = nchoosek(n,k)*p^k*(1-p)^(n-k);
Poisson_PMF(k+1) = ((a^k)/factorial(k))*exp(-a);
end
bar(x,Binomial_PMF())
hold on
grid on
stem(x,Poisson_PMF)
xlabel("k")
ylabel("P[X=k]")
title("Approximation")
legend("Binomial PMF", "Poisson PMF")<result>
비교
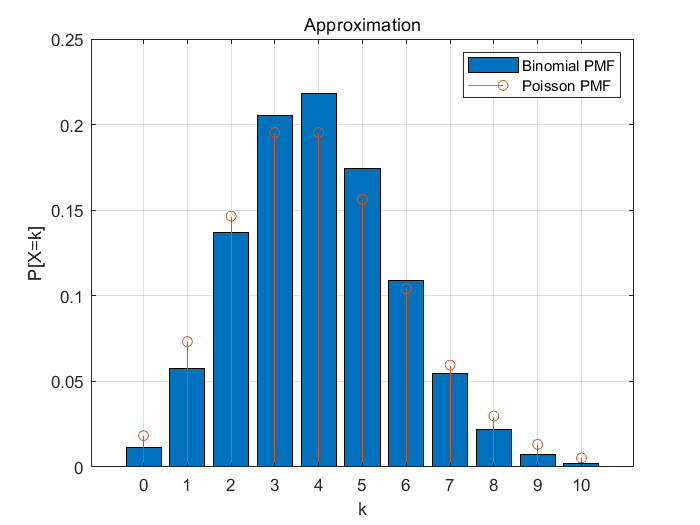
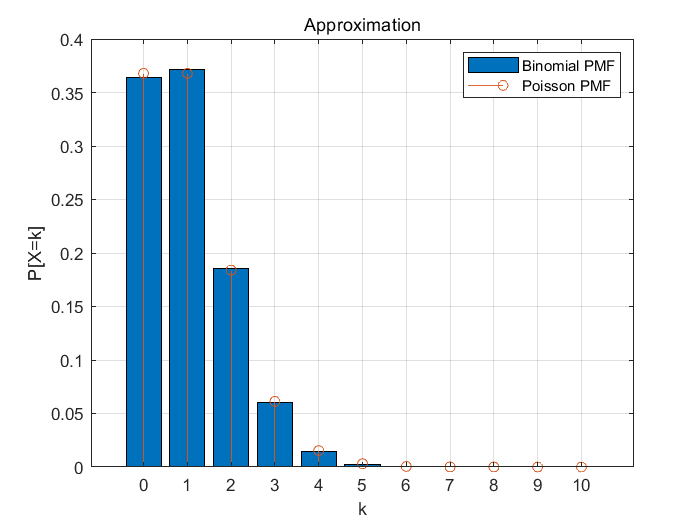
결과를 학인해보면 시행횟수가 적고 확률이 크면 서로 오차가 크지만
시행횟수가 많고 성공할 확률이 매우 적으면 두개는 서로 근사한 값을 가짐을 알 수 있다.
'테크 > MATLAB' 카테고리의 다른 글
| [MATLAB] Exponential Random Variable(지수분포) (1) | 2021.11.01 |
|---|---|
| [MATLAB] 이미지 프로세싱(R, G, B 이진화) (0) | 2021.07.13 |
| [MATLAB] 신호의 주파수 해석(Fourier Analysis in Frequency Domain) (0) | 2021.07.10 |
| [MATLAB] 악보 만들고 연주하기 & 파형분석 (0) | 2021.07.10 |
| [MATLAB] 이미지 분석 & 히스토그램(RGB histogram) (0) | 2021.07.09 |
확률과 통계학 수업을 하면서 여러 확률모델에 관해 배웠다. 그중 이산적(discrete)인 Empirical PMF을 통해 Binomial RV와 Poisson RV를 비교해 보자.
What is
Binomial Random Variable?
Binomial RV란 고등학교 확률과 통계 수업에서 배우는 '이항분포'와 같은 개념이다.
n번의 독립시행중 성공할 확률이 p일 때 갖는 이산확률분포이다.
말로 표현하기에는 와닿지 않으니 바로 PMF를 확인해 보자
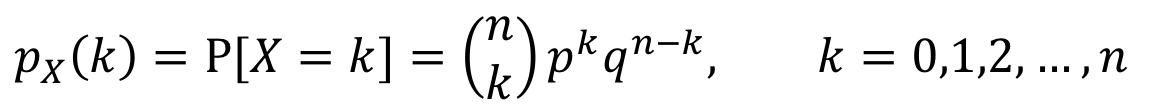
위 식을 해석하자면
총 n번 시행 중
성공할 확률 : p, 실패할 확률 : q (=1-p)
일때 성공을 k번, 실패를 n-k번 발생할 때의 확률을 표현한 식이다.
평균 : E[X] = np
분산 : VAR[X] = npq = np(1-p)
Binomial RV는 매우 general한 형태이다.
n=1이면 Bernoulli(베르누이) RV를 형성하며
n이 많고, p가 적으면 Poisson(포아송) RV를 따른다.
Poisson RV의 PMF는 다음과 같이 표현되는데 과연 Binomial RV로부터 Poisson RV를 도출할 수 있는지 매트랩으로 확인해 보자.
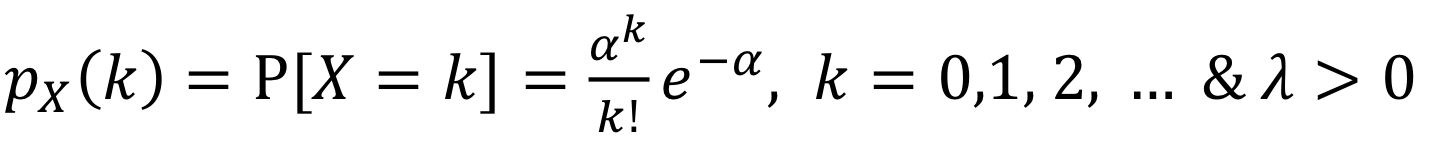
Binomial RV
VS
Poisson RV
앞서 Binomial RV에서 n이 많고 p가 적으면 Poisson RV를 따른다고 했다.
그렇다면 두개의 테스트를 통해
i) n=20, p=0.2
ii) n=50, p=0.02
일때 그래프를 비교해 보자.
n=20, p=0.02 일때
<code>
n=20; #시행횟수
p=0.2; #확률
a = n*p;
x = linspace(0,10,11); #0부터 10까지 11개의 인덱스 생성
Binomial_PMF = linspace(0,10,10);
Poisson_PMF = linspace(0,10,10);
for k = 0:10
Binomial_PMF(k+1) = nchoosek(n,k)*p^k*(1-p)^(n-k);
Poisson_PMF(k+1) = ((a^k)/factorial(k))*exp(-a);
end
bar(x,Binomial_PMF())
hold on
grid on
stem(x,Poisson_PMF)
xlabel("k")
ylabel("P[X=k]")
title("Approximation")
legend("Binomial PMF", "Poisson PMF")<result>

n=50, p=0.02일때
<code>
n=50;
p=0.02;
a = n*p;
x = linspace(0,10,11);
Binomial_PMF = linspace(0,10,10);
Poisson_PMF = linspace(0,10,10);
for k = 0:10
Binomial_PMF(k+1) = nchoosek(n,k)*p^k*(1-p)^(n-k);
Poisson_PMF(k+1) = ((a^k)/factorial(k))*exp(-a);
end
bar(x,Binomial_PMF())
hold on
grid on
stem(x,Poisson_PMF)
xlabel("k")
ylabel("P[X=k]")
title("Approximation")
legend("Binomial PMF", "Poisson PMF")<result>

비교


결과를 학인해보면 시행횟수가 적고 확률이 크면 서로 오차가 크지만
시행횟수가 많고 성공할 확률이 매우 적으면 두개는 서로 근사한 값을 가짐을 알 수 있다.
'테크 > MATLAB' 카테고리의 다른 글
| [MATLAB] Exponential Random Variable(지수분포) (1) | 2021.11.01 |
|---|---|
| [MATLAB] 이미지 프로세싱(R, G, B 이진화) (0) | 2021.07.13 |
| [MATLAB] 신호의 주파수 해석(Fourier Analysis in Frequency Domain) (0) | 2021.07.10 |
| [MATLAB] 악보 만들고 연주하기 & 파형분석 (0) | 2021.07.10 |
| [MATLAB] 이미지 분석 & 히스토그램(RGB histogram) (0) | 2021.07.09 |
