지난번엔 시각적으로 이미지 처리&분석을 했다면 이번에는 청각으로 넘어가 보자.
우리가 듣는 모든 소리는 파형과 진동수를 갖고 있으며 사인, 코사인과 진동수의 조합으로 모든 소리를 재현할 수 있다.
우리가 흔히 접할 수 있는 계이름(도 레 미 파 솔 라 시)도 각각의 주파수(=진동수)를 갖고있다.
| 도 | 262 Hz |
| 레 | 294 Hz |
| 미 | 330 Hz |
| 파 | 349 Hz |
| 솔 | 392 Hz |
| 라 | 440 Hz |
| 시 | 494 Hz |
| (높은)도 | 523 Hz |
(소수점 생략)
가장 기본적인 사인함수인 sin(2*pi*freq*t)형태로 소리를 출력할 수 있다.
또한 같은 사인함수지만 주파수만 다르게 한 후 합하면 화음을 연출 할 수도 있다.
ex) sin(2*pi*262*t) + sin(2*pi*330*t) + sin(2*pi*392*t) = 도+미+솔 화음
그러나 이렇게 계이름 하나하나 전부 sin함수를 나열하면 가독성도 떨어질 뿐만 아니라 나중에 오류가 나면 찾아내기 힘들다.
여기서 sin연산에 관한 함수를 따로 만들어 준 후, 주파수별로 이름을 설정해주면 길이가 확 줄어들게 된다.
또한 계이름 나열한 것을 하나의 row vector형태로 묶어주면 소리출력, 그래프 해석하기도 훨씬 편해진다.
//main함수
fs=4000;
do=262;
dos=277; //도샾
re=294;
mi=330;
fa=349;
fas=370;
sol=392;
la=440;
ti=494;
do1=523;
do1s=554;
re1=587;
mi1=659;
fa1=698;
fa1s=740;
//캐논 악보(화음)
output=[sg_f(fa1s,1)+sg_f(re1,1),sg_f(mi1,1)+sg_f(do1s,1),sg_f(re1,1)+sg_f(ti,1),sg_f(do1s,1)+sg_f(la,1),sg_f(ti,1)+sg_f(sol,1),sg_f(la,1)+sg_f(fas,1),sg_f(ti,1)+sg_f(sol,1),sg_f(do1s,1)+sg_f(mi,1)];
sound(output,fs);맨 위에 선언한 fs=4000은 sampling frequency의 약자이며 1초에 4000번을 sampling한다는 의미이다. 이에 관한 설명은 fourier transform과 함께 다음 포스팅에서 자세히 다루겠다.
//sg_f(sound generator_function)함수
function y=sg_f(freq,time_d)
t=linspace(0,1,4000*time_d);
y=sin(2*pi*freq*t);위의 코드를 실행하면 sound() 함수로 인해 코딩한 대로 캐논 화음이 연주된다.
그러나 단순히 sin형태로만 구성이 되어 있어서 다소 딱딱한 기계음으로 연주를 해서 듣기 썩 편하진 않다.
이를 보완하기 위해 sin함수와 exponential(지수함수)의 조합으로 선율을 부드럽게 만들 수 있다.
선율을 바꾸기 위한 함수를 따로 만든 후 sg_f에서 호출하는 방식으로 구성한다.
//피아노 소리
function output=ufunc(freq, t)
output=0.6*sin(2*pi*freq*t).*exp(-4*t);
output=output+0.4*sin(2*2*pi*freq*t).*exp(-4*t);
output=output+0.3*sin(3*2*pi*freq*t).*exp(-4*t);(위, 아래의 함수는 각각 다른 함수이기 때문에 서로 다른 스크립트 파일에서 작성해야 한다.)
//sg_f함수(ufunc호출)
function y=sg_f(freq,time_d)
t=linspace(0,1,4000*time_d);
y=ufunc(freq,t);위의 소리는 sin(2*pi*freq*t)로만 구성한 음색인 반면
아래는 sin의 내부적인 복잡한 연산과 exp의 조합으로 더욱 부드러운 음색을 보여준다.
exp(-4*t)에서 -로 인해 지수함수적으로 소리가 점점 줄어드는 것 또한 확인 할 수 있다.
파형 분석
이제 소리도 출력했겠다 내가 만든 음악의 파형을 보자!
일단 처음 확인하는것이니 sin함수로만 구성된 음악을 보자.
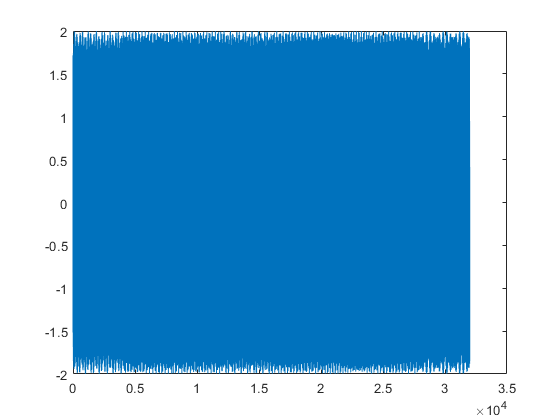
이게 뭐요....내가 생각한건 이게 아닌데.....근데 위아래를 자세히 보면 노이즈가 있다? 확대를 해보자.
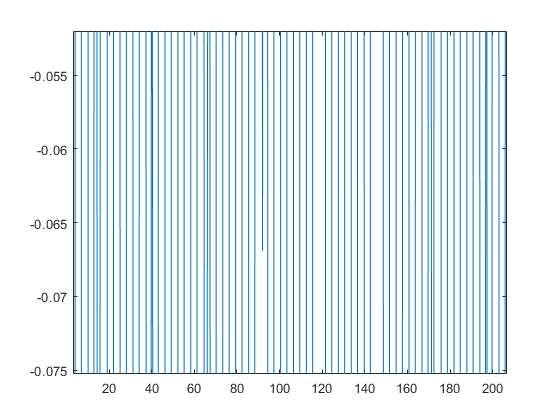
자세히 보니 뭐가 끊어지는것 같다...?그렇다면 xlim()을 통해서 일정 구간만 확인해보자.
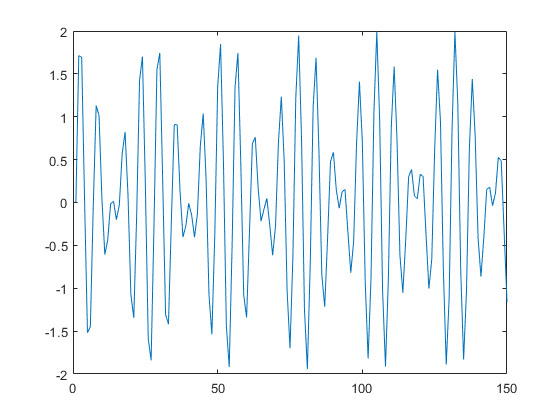
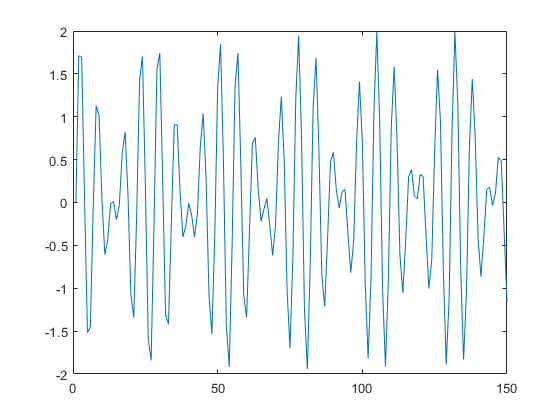
오!!이것이 내가 만든 캐논의 파형!! 화음에서 sin함수 두개를 더했기 때문에 들쭉날쭉한 모습을 보이지만 역시 주기를 갖고있음을 확인 할 수 있다.
그럼 이제 피아노소리를 만든함수 즉 복잡한 연산은 파형이 어떻게 나올까??
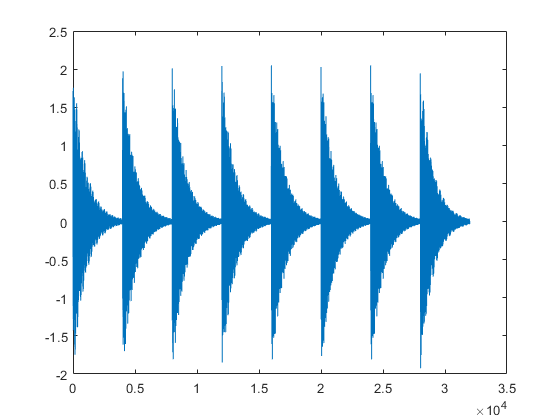
오....역시 exp로 인해 음 하나하나가 점점 지수함수적으로 감소되는 모습이 보인다.
그럼 이것도 xlim을 통해서 확인해보면?
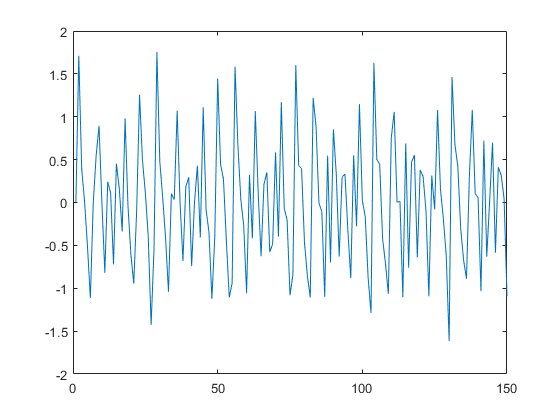
이것이 바로 피아노소리와 흡사한 음파의 형태구나!
단일 sin파와 비교해보면 나름 고른 모습을 보이고 위아래로 튀는 신호도 없다. 즉 노이즈가 적게 발생한 것이고 우리에게 더욱 듣기 좋은 소리를 들려준다.
다음은 이 시간영역 신호를 주파수 영역으로 해석하는 fourier transform에 관해 얘기하고 주파수 해석도 해보자.
'테크 > MATLAB' 카테고리의 다른 글
| [MATLAB] 이미지 프로세싱(R, G, B 이진화) (0) | 2021.07.13 |
|---|---|
| [MATLAB] 신호의 주파수 해석(Fourier Analysis in Frequency Domain) (0) | 2021.07.10 |
| [MATLAB] 이미지 분석 & 히스토그램(RGB histogram) (0) | 2021.07.09 |
| [MATLAB] 그래프 설정 명령어 (0) | 2021.07.07 |
| [MATLAB] 3D그래프 그리기(Gaussian Distribution Graph 2D & 3D) (1) | 2021.07.06 |