지금까지 우리는 신호를 시간축에 따른 결과값 즉 time domain관점에서 해석했다.
시간에 대한 해석은 그저 파형이 어떻게 생겼는지 관측만 가능 할 뿐 해당 신호의 물리량 및 에너지를 확인 할 수 없다.
이런 신호를 가공하고 처리하기 위해서는 다양한 방법이 있지만 이번 시간에는 여러 방법중 하나인 푸리에 변환(Fourier Transform)에 관해 이야기 하겠다.
푸리에 변환(Fourier Transform)이란?
특정 신호를 시간에 대한 해석이 아닌 주파수에 대한 해석을 하기 위한 변환과정이다.
즉 시간에 대한 그래프는 x축 : 시간(time), y축 : 크기(magnitude)로 표현하는 반면
주파수에 대한 그래프는 x축 : 주파수(frequenct), y축 : 크기 로 나타낸다.

이런 변환을 해줘야 특정 신호를 변조, 증폭 등 다양한 가공을 할 수 있다.
푸리에 변환을 해주면 수의 단위도 바뀌게 된다.
일반적인 실수형태로 딱 떨어지는 형태가 아닌 실수부+허수부 형태로 상당히 복잡한 형태의 물리량을 갖고 있다.
실제로 그러한지 매트랩의 연산을 통해 확인해 보자.


위의 Time domain에서는 실수형태로만 출력되는 반면
아래 Frequency domain에서는 실수+허수(i) 형태로 출력하는것을 확인 할 수 있다.

fft()함수란 fast fourier transform의 약자로 고속푸리에변환 을 의미한다. 이는 단지 푸리에 변환을 빠르게 처리하는 알고리즘을 내장한 함수이다.
이제 이 결과값들을 샘플링하면 그래프로 나타낼 수 있다.
Sampling Frequency
여기서 샘플링 주파수(sampling frequency)의 개념이 상당히 중요하다.
샘플링 주파수란 1초동안 몇번의 데이터값을 추출해서 그래프에 그릴건지 결정하는 요소이다.
일반적인 mp3, m4a파일은 1초에 44100번의 데이터 추출해서 우리의 귓속으로 들어온다.
하지만 지금 당장 고음질의 음원을 발매하는것이 아니기 때문에 많은 데이터를 다룰 필요가 없다.
그래서 간단히 1초에 4000번만 추출하고 확인해 보자.
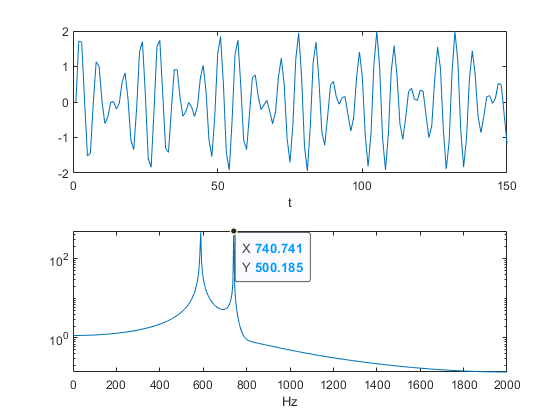
위에는 time domain, 아래는 frequency domain그래프이다.
아래 그래프에서 제일 최고점에 있는 값을 확인해 보면 x축이 740.7라고 나오는데 이 값이 바로 공진주파수 이다.
외부에서 공진주파수와 같은 크기의 주파수를 주면 하모닉스라는 소리가 나며 다른 신호보다 상당한 에너지를 갖게 된다.
만일 건물의 공진주파수와 동일한 충격을 계속 가해주면 건물이 붕괴될 위험이 있어 신호해석에 있어서 공진주파수는 매우 중요하다.
이 신호에서 공진주파수는 740.7Hz이며 공명은 높은파샾이다.
Time & Frequency 동시에 확인가능?
시간에 따른 주파수의 변화도 얼마든지 확인 가능하다. (매트랩의 한계는 어디까지인가....)
spectrogram()이라는 함수를 사용하면 된다.

가로축은 frequency, 세로축은 time으로 시간별로 주파수의 변화를 직관적으로 확인 할 수 있다.
노란 띠가 출력되는 음이며, 시간별로 띠가 두개인 이유는 화음을 넣었기 때문이다.
최 종
소스코드
main
//main 함수
fs=4000;
do=262;
dos=277;
re=294;
mi=330;
fa=349;
fas=370;
sol=392;
la=440;
ti=494;
do1=523;
do1s=554;
re1=587;
mi1=659;
fa1=698;
fa1s=740;
output=[sg_f(fa1s,1)+sg_f(re1,1),sg_f(mi1,1)+sg_f(do1s,1),sg_f(re1,1)+sg_f(ti,1),sg_f(do1s,1)+sg_f(la,1),sg_f(ti,1)+sg_f(sol,1),sg_f(la,1)+sg_f(fas,1),sg_f(ti,1)+sg_f(sol,1),sg_f(do1s,1)+sg_f(mi,1)];
output1=[sg_f(fa1s,0.5)+sg_f(re1,0.5),sg_f(mi1,0.5)+sg_f(do1s,0.5),sg_f(re1,0.5)+sg_f(ti,0.5),sg_f(do1s,0.5)+sg_f(la,0.5),sg_f(ti,0.5)+sg_f(sol,0.5),sg_f(la,0.5)+sg_f(fas,0.5),sg_f(ti,0.5)+sg_f(sol,0.5),sg_f(do1s,0.5)+sg_f(mi,0.5)];
sound(output,fs);
subplot(3,1,1);
plot(output);
xlim([0,150]);
xlabel('t');
subplot(3,1,2);
input=output(1:1000);
f_axis=linspace(0,4000,1000);
fft(input);
semilogy(f_axis,abs(fft(input)));
xlim([0,2000]);
xlabel('Hz');
subplot(3,1,3);
spectrogram(output,1024,1000,1024,4000);sg_f.m(function)
function y=sg_f(freq,time_d)
t=linspace(0,1,4000*time_d);
y=ufunc(freq,t);ufunc.m(function)
function output=ufunc(freq,t)
%% 기본
output=sin(2*pi*freq*t);
%% 피아노 소리
%output=sin(2*pi*freq*t).*exp(-7*t);
% output=sin(2*pi*freq*t);
% output=0.6*sin(2*pi*freq*t).*exp(-4*t);
% output=output+0.4*sin(2*2*pi*freq*t).*exp(-4*t);
% output=output+0.3*sin(3*2*pi*freq*t).*exp(-4*t);
%% 피아노 소리
% output=sin(2*pi*freq*t).*exp(-0.0004*2*pi*freq*t);
% output=output+sin(2*2*pi*freq*t).*exp(-0.0004*2*pi*freq*t)/2;
% output=output+sin(3*2*pi*freq*t).*exp(-0.0004*2*pi*freq*t)/4;
% output=output+sin(4*2*pi*freq*t).*exp(-0.0004*2*pi*freq*t)/8;
% output=output+sin(5*2*pi*freq*t).*exp(-0.0004*2*pi*freq*t)/16;
% output=output.*output.*output;
% output=output+0.1*sawtooth(2*pi*freq*t);
출력화면


'테크 > MATLAB' 카테고리의 다른 글
| [MATLAB] 이산확률변수(Discrete Random Variable) (0) | 2021.10.31 |
|---|---|
| [MATLAB] 이미지 프로세싱(R, G, B 이진화) (0) | 2021.07.13 |
| [MATLAB] 악보 만들고 연주하기 & 파형분석 (0) | 2021.07.10 |
| [MATLAB] 이미지 분석 & 히스토그램(RGB histogram) (0) | 2021.07.09 |
| [MATLAB] 그래프 설정 명령어 (0) | 2021.07.07 |
