Entropy / Cross-Entropy
엔트로피란 물리에서 '무질서도'를 가리키는 용어이지만 확률, 딥러닝분야에선 정보를 표현하는데 필요한 최소 평균 자원량(bit수)를 의미한다.
엔트로피를 통해서 알 수 있는 정보는
1. 엔트로피는 가장 최적의 방식으로 코딩했을 때 비트수를 나타낸다.
2. 엔트로피보다 더 짧게 코딩할 수 없다.
일반적인 엔트로피 수식은 다음과 같다.

여기서 pk는 '실제확률'를 의미하며 확률이 크면 짧게 코딩하고, 확률이 작으면 길게 코딩하는것이 효율적이라고 한다.
표본 샘플의 확률이 전부 동일하면 엔트로피가 최대값이 나오게된다. 이는 곧 비트수가 최대가 된다는 의미이며 결국 최악의 경우가 된다는 뜻이다.
반면, 샘플의 확률이 각각 달라서 특정 확률에 치우쳐져 있다면 엔트로피는 작게 나오게 되며 비트수도 줄어들게 되므로 좋은 case라고 볼 수 있다.
그러나 실제 딥러닝에서 일반적인 entropy 보다 cross entropy를 더 많이 이용한다고 한다.
Cross-Entropy
크로스 엔트로피는 예측확률과 실제확률의 차이로부터 오차를 계산해서 보다 정확한 학습을 할 수 있다.
엔트로피와 크로스엔트로피를 비교해보면 크로스엔트로피의 비트값이 더 크지만 최적화가 잘 되어있다고 한다.
크로스엔트로피의 수식은 다음과 같다.

qx가 예측확률분포, pi가 실제(정답)확률분포를 의미한다.
따라서 두 분포(예측, 실제)가 동일하면 Cross-entropy error는 0에 가까워 진다.
Cross-Entrypy-Error를 이용한 MNIST학습 실습
실습 코드는 지난번에 다뤘던 mse코드에서 MSELoss(mean square error loss)부분을 CrossEntropyLoss()로 바꿔주기만 하고 실행을 해보자.

mse에서 10회째 정확도가 86.88%로 나왔었지만 cee로 학습한 결과 90.12%의 정확도를 보여준다.
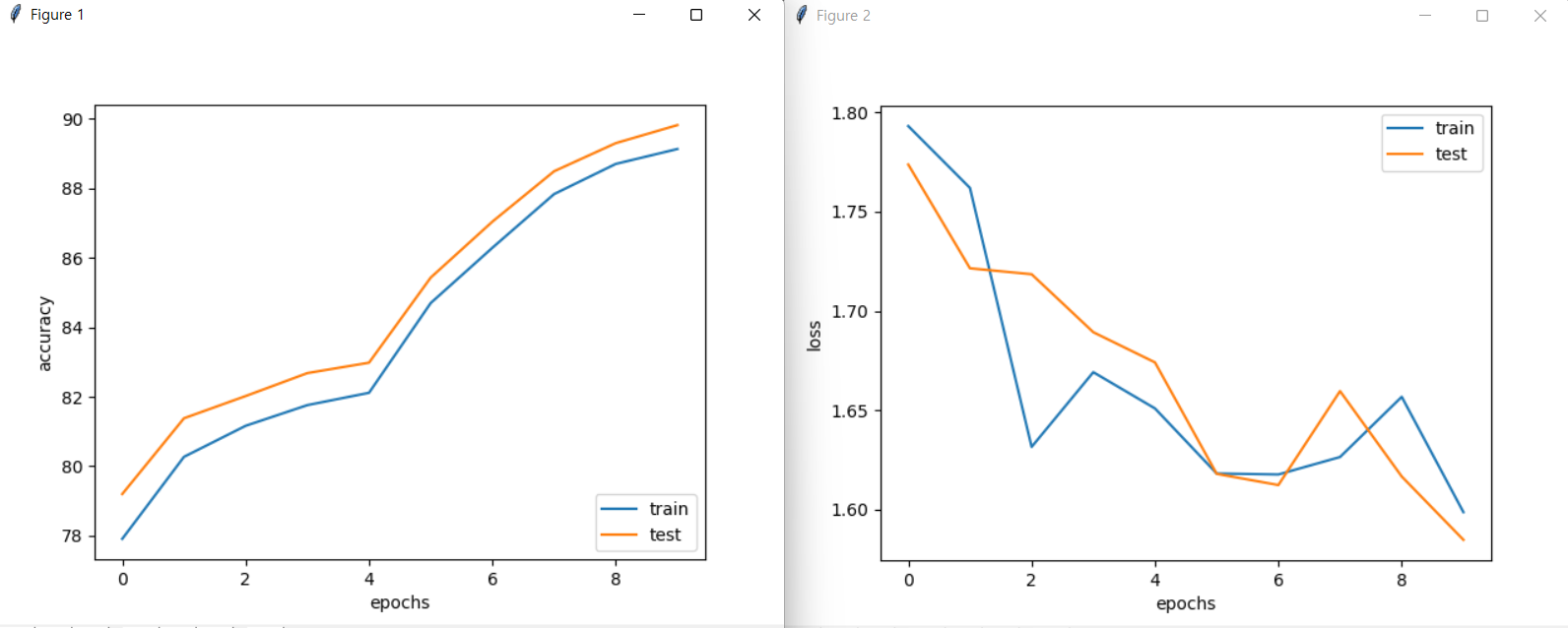
mse보다 더 높은 정확도를 보이지만 아직도 부족하다.
다음엔 더 높은 정확도와 에러를 줄일 수 있는 fully connected layers를 다뤄보자.
'테크 > ML | DL' 카테고리의 다른 글
| [ML] 선형회귀와 경사하강법 (0) | 2022.11.03 |
|---|---|
| [ML / DL] MNIST 학습모델 (0) | 2022.02.16 |
| [ML/DL] 경사 하강법 SGD 실습(with.python) (0) | 2022.02.16 |
| [ML/DL] 딥러닝 기본 개념 (0) | 2022.02.15 |
