딥러닝을 배울때 기본적으로 알고있어야 하는 지식이 상당히 많다.
2학년을 마치고 딥러닝을 배우고 나서야 대학에서 배운 수학이 인공지능에서 어떻게 쓰이는지 알게 되었다.
AI를 배우기 위해 선형대수(행렬), 확률과통계, 미적분은 필수로 알고있어야 한다.
error == loss == 오차 == 손실 != 오류
딥러닝에서 사용하는 error라는 용어는 우리가 일반적으로 아는 오류 라는 의미가 아닌 오차라는 뜻을 갖는다.
오차는 다른말로 error, loss, 손실이라고도 부른다.
가중치
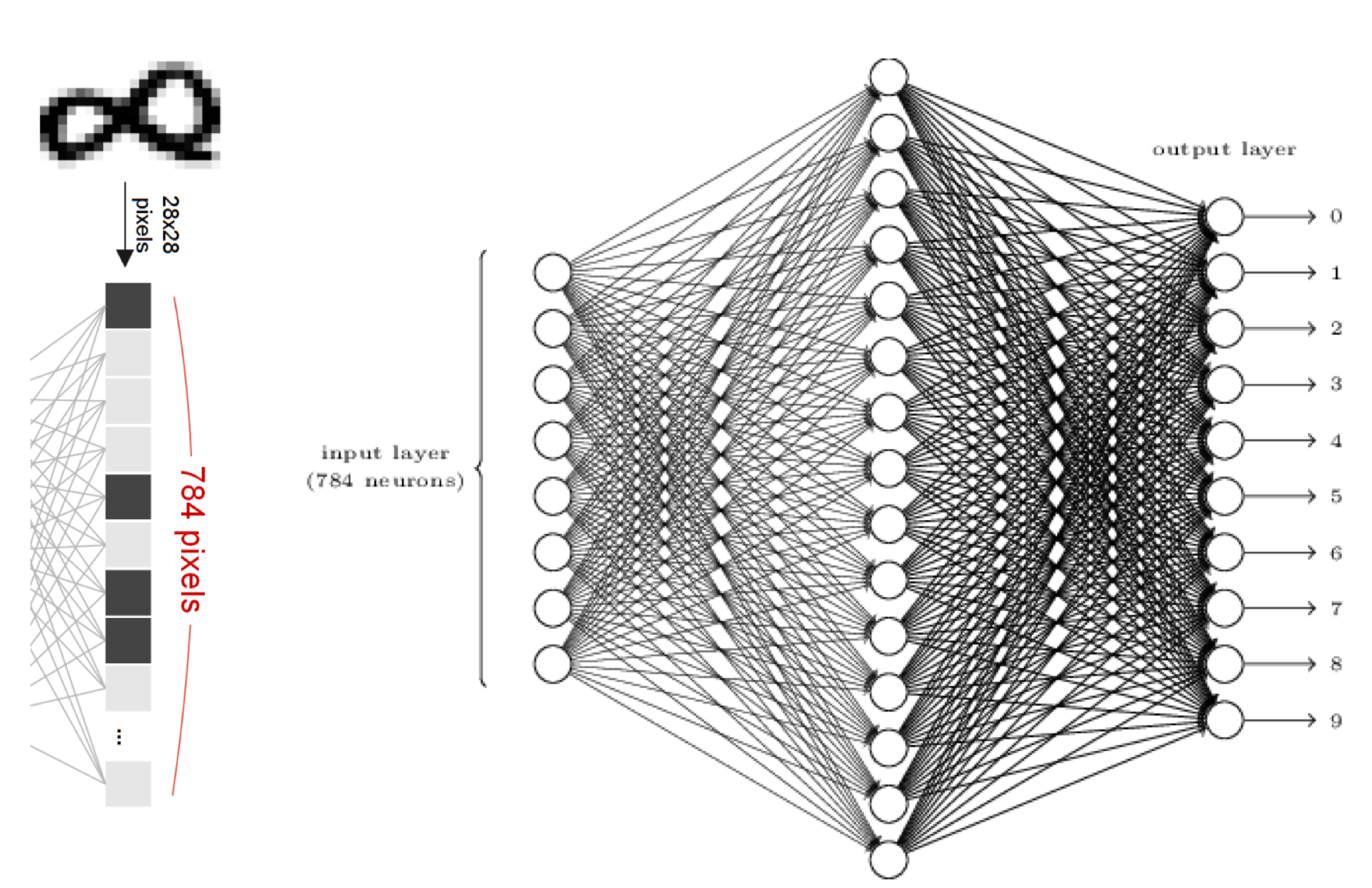
숫자를 인식하는 신경망을 예로 들어보자.
8이라는 숫자 이미지는 28x28=784개의 픽셀로 구성되어 있다고 가정하자.
그러면 input으로 784개의 데이터를 입력해 주어야 한다.
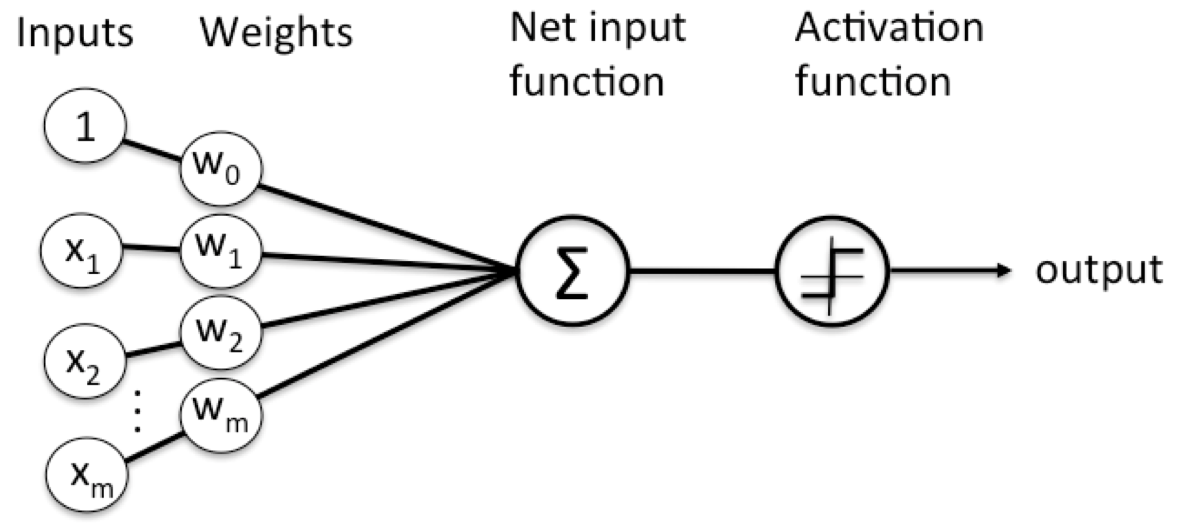
input layer에 784개의 뉴런이 있으며 각각의 뉴런은 input데이터와 가중치를 곱하고 총 합을 더해서 개발자가 생성한 hidden layer을 통해 학습을 하게 된다.
hidden layer에서는 activation function을 거쳐서 우리가 원하는 output으로 출력하게 된다.
이런 과정을 정리하면 다음과 같다.
선형회귀
일반적으로 딥러닝을 시작할때 선형회귀모델을 가장 많이 시작한다.
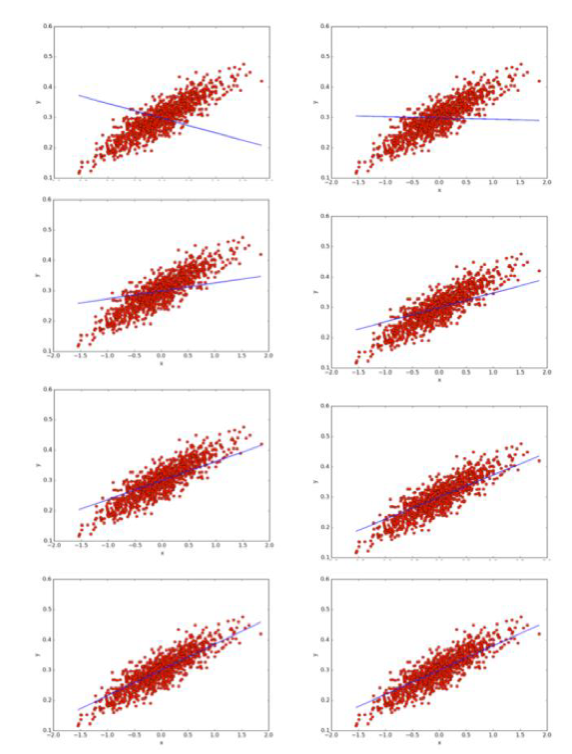
위의 이미지는 컴퓨터가 왼쪽 위에서부터 오른쪽 아래로 학습을 하는 모습을 나타낸다.
수많은 점은 주어진 값이며 해당 점이 분포된 평균치를 컴퓨터가 스스로 학습하는 과정이다.
따라서 직선을 나타내는데 이 직선이 수많은 점의 평균치를 찾아내야 하며 이를 '선형회귀' 라고 한다.
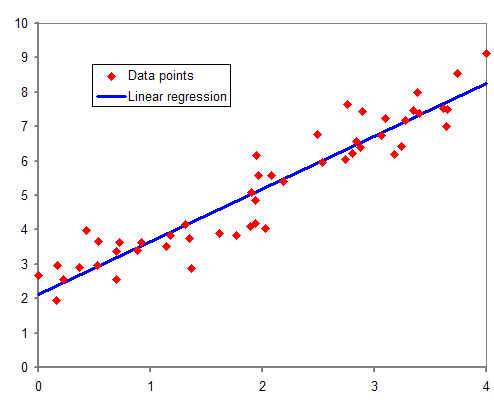
직선은 일반적으로 (y=ax + b)와 같은 꼴로 나타내지만 우리에겐 기울기가 중요하기 때문에 (y = ax)라고 표현하자.
이제 MSE를 통해서 어떻게 최적의 기울기를 찾아낼 수 있는지 알아보자.
MSE
(Mean Square Error)
MSE는 선형대수부터 공업수학, 전자회로 등 다양한 학문에 등장해 괴롭힌 경험이 있어서 잊을수가 없는 개념이다.
이름에서 알 수 있듯이
mean : 평균
square : 제곱
error : 오차
평균을 제곱해서 오차를 구한다는 뜻이다.
이를 증명하는 방법은 많지만 그중 딥러닝에서 왜, 어떻게 사용되는지 알아보자.
선형회귀에서 다룬 직선그래프에서 주어진 값과 추세선의 오차가 2가지 방식이 나온다.
양수(y - y') : 추세선보다 오차가 더 위에 있는 경우
음수(y' - y) : 오차가 추세선보다 아래에 있는 경우
음수는 data로 활용할 수 없기 때문에 제곱을 한 후 모든 input값을 더한 다음 input갯수만큼 나누면 바로 MSE가 된다.
수식으로 표현하면 다음과 같다.
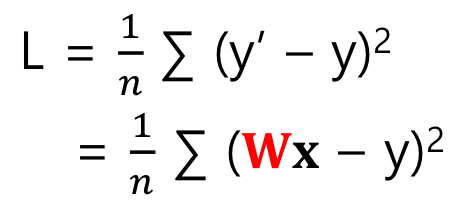
y는 우리가 구할 추세선(1차 방정식)이기 때문에 Wx라고 치환할 수 있게되며 여기서 n, x, y는 주어진 값, 변하지 않는 값 즉 상수이기 때문에 최종적으로 L = W^2이라고 표현할 수 있다.
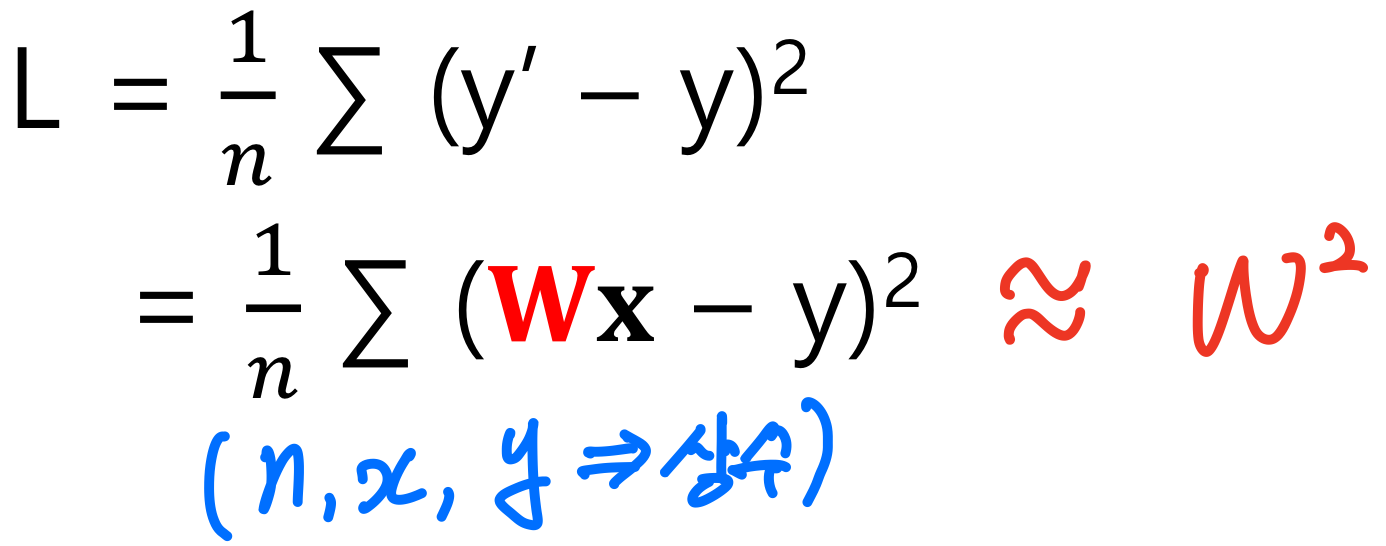
아이러니하게 최적의 1차함수 기울기를 구하기 위해 2차함수를 이용해야 한다.
다음은 이런 수식을 이용한 확률적 경사하강법(SGD)에 대해서 알아보자.
'테크 > ML | DL' 카테고리의 다른 글
| [ML] 선형회귀와 경사하강법 (0) | 2022.11.03 |
|---|---|
| [ML/DL] Cross-Entropy를 이용한 MNIST (0) | 2022.02.17 |
| [ML / DL] MNIST 학습모델 (0) | 2022.02.16 |
| [ML/DL] 경사 하강법 SGD 실습(with.python) (0) | 2022.02.16 |
딥러닝을 배울때 기본적으로 알고있어야 하는 지식이 상당히 많다.
2학년을 마치고 딥러닝을 배우고 나서야 대학에서 배운 수학이 인공지능에서 어떻게 쓰이는지 알게 되었다.
AI를 배우기 위해 선형대수(행렬), 확률과통계, 미적분은 필수로 알고있어야 한다.
error == loss == 오차 == 손실 != 오류
딥러닝에서 사용하는 error라는 용어는 우리가 일반적으로 아는 오류 라는 의미가 아닌 오차라는 뜻을 갖는다.
오차는 다른말로 error, loss, 손실이라고도 부른다.
가중치

숫자를 인식하는 신경망을 예로 들어보자.
8이라는 숫자 이미지는 28x28=784개의 픽셀로 구성되어 있다고 가정하자.
그러면 input으로 784개의 데이터를 입력해 주어야 한다.
input layer에 784개의 뉴런이 있으며 각각의 뉴런은 input데이터와 가중치를 곱하고 총 합을 더해서 개발자가 생성한 hidden layer을 통해 학습을 하게 된다.
hidden layer에서는 activation function을 거쳐서 우리가 원하는 output으로 출력하게 된다.
이런 과정을 정리하면 다음과 같다.

선형회귀
일반적으로 딥러닝을 시작할때 선형회귀모델을 가장 많이 시작한다.

위의 이미지는 컴퓨터가 왼쪽 위에서부터 오른쪽 아래로 학습을 하는 모습을 나타낸다.
수많은 점은 주어진 값이며 해당 점이 분포된 평균치를 컴퓨터가 스스로 학습하는 과정이다.
따라서 직선을 나타내는데 이 직선이 수많은 점의 평균치를 찾아내야 하며 이를 '선형회귀' 라고 한다.

직선은 일반적으로 (y=ax + b)와 같은 꼴로 나타내지만 우리에겐 기울기가 중요하기 때문에 (y = ax)라고 표현하자.
이제 MSE를 통해서 어떻게 최적의 기울기를 찾아낼 수 있는지 알아보자.
MSE
(Mean Square Error)
MSE는 선형대수부터 공업수학, 전자회로 등 다양한 학문에 등장해 괴롭힌 경험이 있어서 잊을수가 없는 개념이다.
이름에서 알 수 있듯이
mean : 평균
square : 제곱
error : 오차
평균을 제곱해서 오차를 구한다는 뜻이다.
이를 증명하는 방법은 많지만 그중 딥러닝에서 왜, 어떻게 사용되는지 알아보자.
선형회귀에서 다룬 직선그래프에서 주어진 값과 추세선의 오차가 2가지 방식이 나온다.
양수(y - y') : 추세선보다 오차가 더 위에 있는 경우
음수(y' - y) : 오차가 추세선보다 아래에 있는 경우
음수는 data로 활용할 수 없기 때문에 제곱을 한 후 모든 input값을 더한 다음 input갯수만큼 나누면 바로 MSE가 된다.
수식으로 표현하면 다음과 같다.
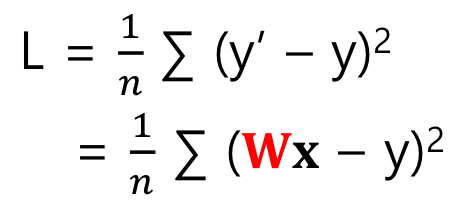
y는 우리가 구할 추세선(1차 방정식)이기 때문에 Wx라고 치환할 수 있게되며 여기서 n, x, y는 주어진 값, 변하지 않는 값 즉 상수이기 때문에 최종적으로 L = W^2이라고 표현할 수 있다.
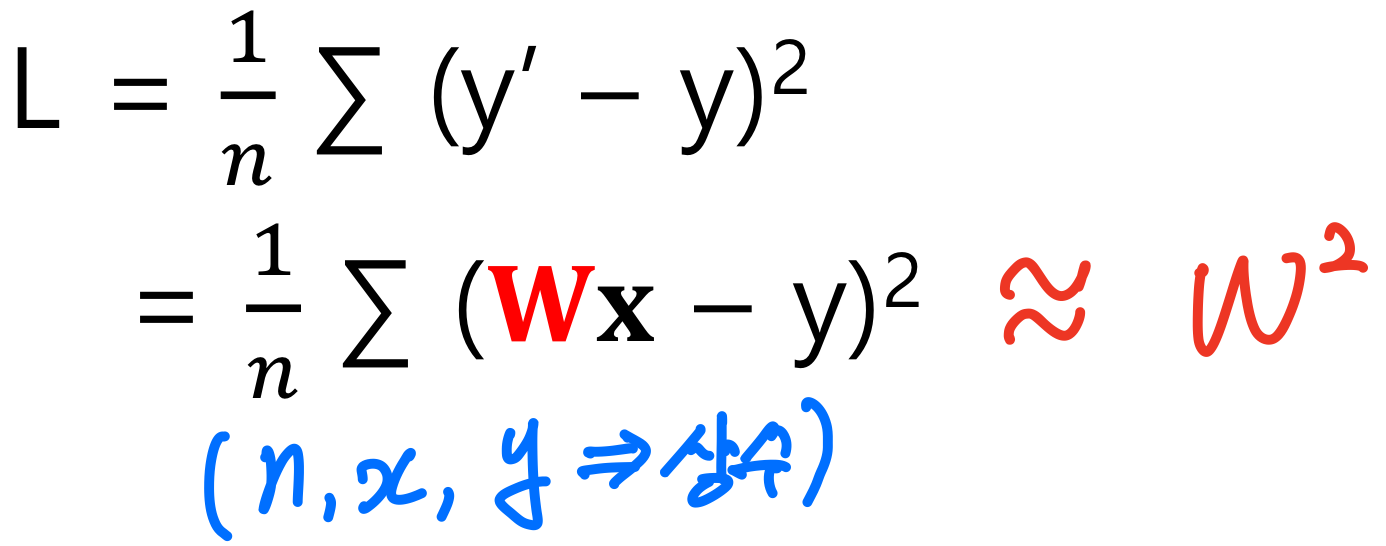
아이러니하게 최적의 1차함수 기울기를 구하기 위해 2차함수를 이용해야 한다.
다음은 이런 수식을 이용한 확률적 경사하강법(SGD)에 대해서 알아보자.
'테크 > ML | DL' 카테고리의 다른 글
| [ML] 선형회귀와 경사하강법 (0) | 2022.11.03 |
|---|---|
| [ML/DL] Cross-Entropy를 이용한 MNIST (0) | 2022.02.17 |
| [ML / DL] MNIST 학습모델 (0) | 2022.02.16 |
| [ML/DL] 경사 하강법 SGD 실습(with.python) (0) | 2022.02.16 |
