[ML / DL] MNIST 학습모델
MNIST
(Modified National Institute of Standards and Technology)
MNIST란 손으로 쓴 숫자를 기계학습을 통해서 인식하도록 하는 모델이다.
MNIST데이터 베이스에 60,000개의 트레이닝 이미지와 10,000개의 테스트 이미지가 있어서 이를 활용하면서 기계학습을 시켜나갈 수 있다.

MNIST handwritten digit database, Yann LeCun, Corinna Cortes and Chris Burges
MNIST handwritten digit database, Yann LeCun, Corinna Cortes and Chris Burges
yann.lecun.com
신경망 구성
MNIST데이터셋을 이용한 기계학습은 input layer와 output layer로만 구성되어 있지만 input layer를 제외해서 총 1 layer neural network로 구성된다. 1 layer만 존재하기 때문에 결과를 출력할때 학습한 것을 분류만 하면 되는데 이때 사용되는 activation function은 softmax함수를 사용한다.
Softmax function(activation function)
소프트 맥스 함수의 수식은 다음과 같다.
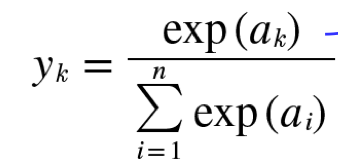
처음 보면 상당히 머리하프게 생겼지만 그 의미를 알면 별거 없다.
분모는 모든 input신호의 지수함수의 총합, 분수는 input신호의 지수함수이다.
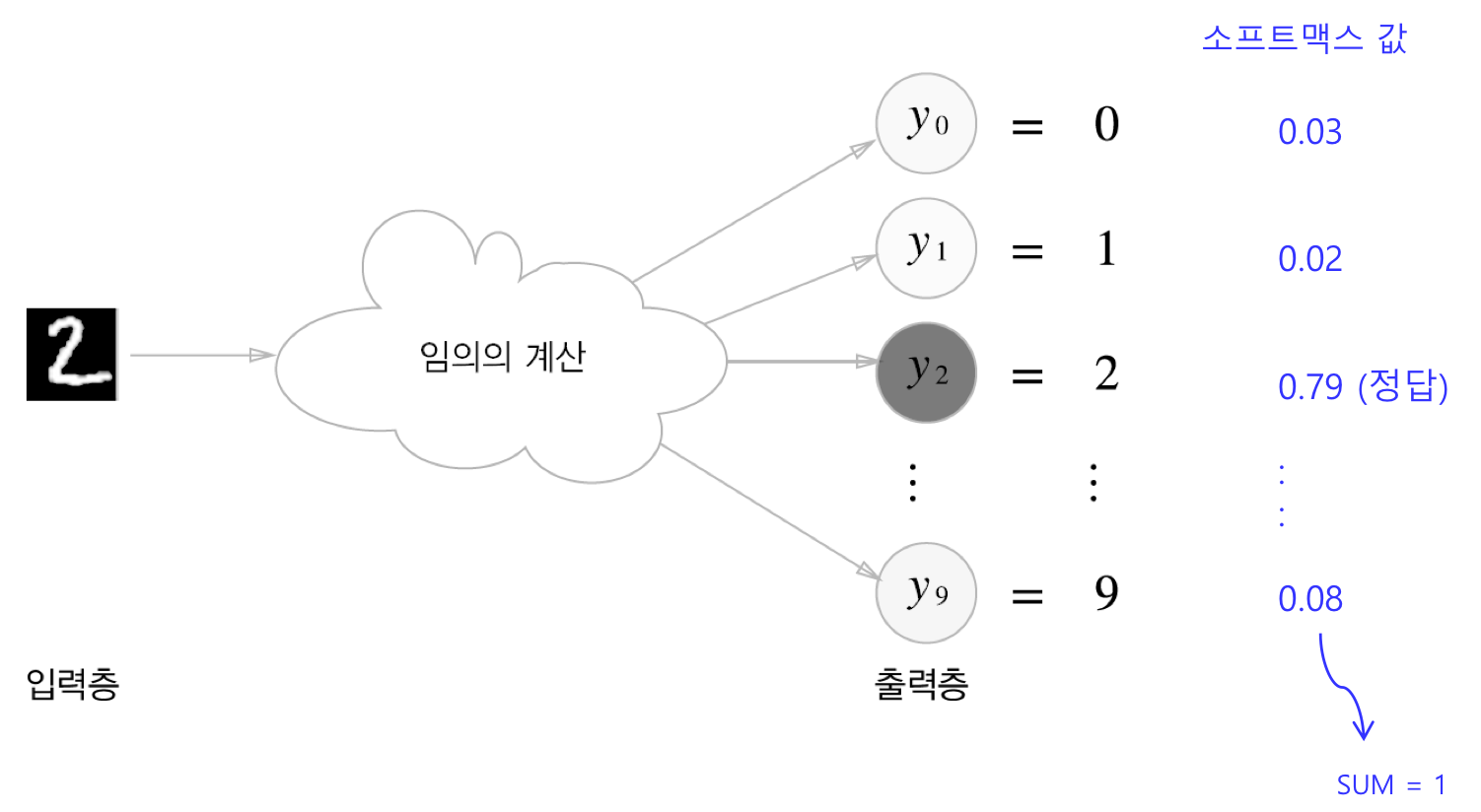
이를 보아 결과는 비율로 나타나며 최종 결과의 총 합은 1이 된다.
결국엔 모든 출력을 확률로 환산이 가능하다는 뜻이며 확률이 가장 큰 값이 정답이 되는 셈이다.
따라서 모든 학습데이터의 최종 분류는 softmax함수를 통해 분류가 된다.
실제 코드에서 softmax연산은 input data과 weight를 곱한다음 bias를 더한 결과가 output으로 나온다.
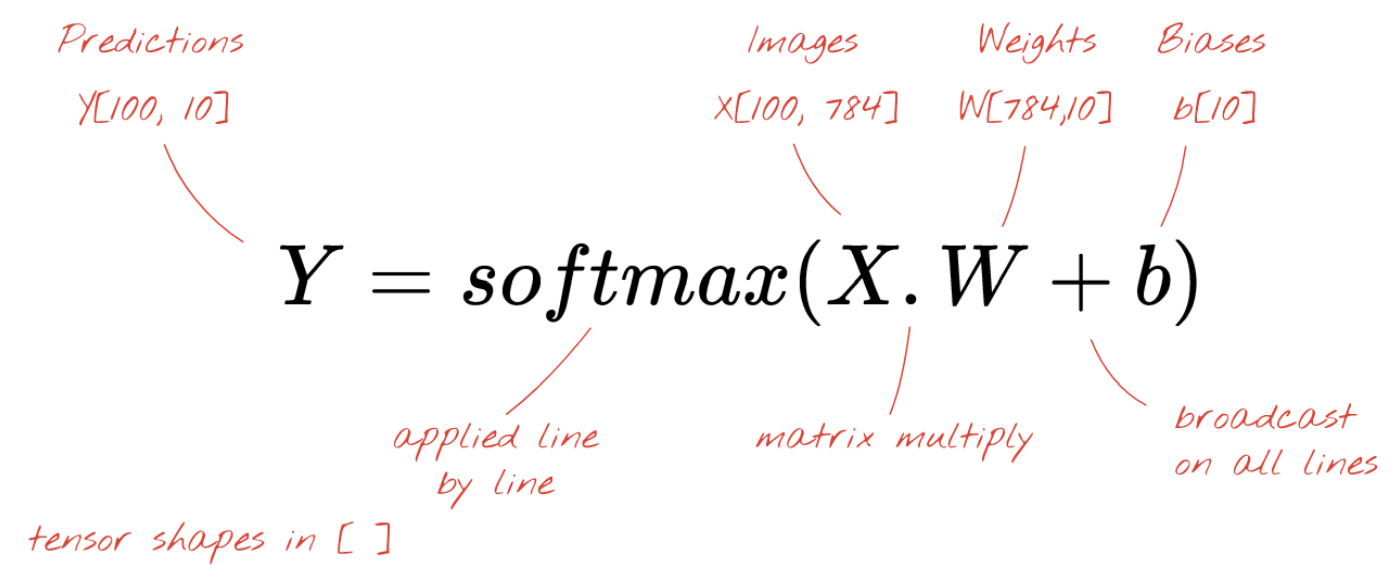
MNIST 학습 실행
위에서 설명한 1 layer 짜리 모델을 구현시킨 코드는 다음과 같다.
# Imports
import torch
import torchvision
import torch.nn as nn # All neural network modules, nn.Linear, nn.Conv2d, BatchNorm, Loss functions
import torch.optim as optim # For all Optimization algorithms, SGD, Adam, etc.
import torch.nn.functional as F # All functions that don't have any parameters
from torch.utils.data import DataLoader # Gives easier dataset managment and creates mini batches
import torchvision.datasets as datasets # Has standard datasets we can import in a nice way
import torchvision.transforms as transforms # Transformations we can perform on our dataset
def check_accuracy(loader, model, criterion):
if loader.dataset.train:
mode = 'train'
else:
mode = 'test '
model.eval()
num_correct = 0
num_samples = 0
with torch.no_grad():
for x, y in loader:
x = x.to(device=device)
y = y.to(device=device)
x = x.reshape(x.shape[0], -1)
predictions = model(x) # tensor([[ 1.2100e-01, -3.0610e-02, 1.3518e-01, -6.9840e-02, 3.5525e-01, 1.2030e-02, -8.2505e-02, 1.8832e-01, -7.2998e-02, 1.0412e-01],
probs, predictions = predictions.max(1) # refer torch.max -> probs = tensor([0.35525,...]), predictions = tensor([4,...])
num_correct += (predictions == y).sum()
num_samples += predictions.size(0)
accuracy = float(num_correct)/float(num_samples)*100
# get loss
predictions = model(x)
y = torch.nn.functional.one_hot(y, num_classes=10)
y = y.to(torch.float32)
loss = criterion(predictions, y)
loss = loss.item() # tensor -> value
print(
# f'{mode} : accuracy = {float(num_correct)/float(num_samples)*100:.2f}'
f"{mode} : {num_correct} / {num_samples} with accuracy {accuracy:.2f}"
)
model.train()
return accuracy, loss
def draw_graph(train_accuracy_list, train_loss_list, test_accuracy_list, test_loss_list):
# draw graph : accuracy
x = np.arange(len(train_accuracy_list))
plt.figure(1)
plt.plot(x, train_accuracy_list, label='train', markevery=1)
plt.plot(x, test_accuracy_list, label='test', markevery=1)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.legend(loc='lower right')
# plt.show()
# draw graph : loss
# x = np.arange(len(train_loss_list))
plt.figure(2)
plt.plot(x, train_loss_list, label='train', markevery=1)
plt.plot(x, test_loss_list, label='test', markevery=1)
plt.xlabel("epochs")
plt.ylabel("loss")
plt.legend(loc='upper right')
plt.show()
# Create Fully Connected Network
class NN(nn.Module):
def __init__(self, input_size, num_classes):
super(NN, self).__init__()
self.fc1 = nn.Linear(input_size, num_classes)
def forward(self, x):
x = x.reshape(x.shape[0], -1) # flatten data : 28x28 -> 784, x = x.view(-1,784)
x = F.softmax(self.fc1(x))
return x
if __name__ == '__main__':
# Set device
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Hyperparameters
# input_size = 784
# num_classes = 10
# learning_rate = 0.05
# batch_size = 100
num_epochs = 10
# Load Data
train_dataset = datasets.MNIST(root="dataset/", train=True, transform=transforms.ToTensor(), download=True)
train_loader = DataLoader(dataset=train_dataset, batch_size=100, shuffle=True)
test_dataset = datasets.MNIST(root="dataset/", train=False, transform=transforms.ToTensor(), download=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=100, shuffle=True)
# Initialize nerual network
model = NN(input_size=784, num_classes=10).to(device)
# define Loss and optimizer
loss_criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.05)
# Train model
train_accuracy_list = []
train_loss_list = []
test_accuracy_list = []
test_loss_list = []
for epoch in range(num_epochs):
for batch_idx, (input_image, targets) in enumerate(train_loader):
# Get input_image to CPU/cuda
input_image = input_image.to(device=device)
targets = torch.nn.functional.one_hot(targets, num_classes=10)
targets = targets.to(torch.float32)
targets = targets.to(device=device)
# predict(forward)
predictions = model(input_image)
# loss 계산
loss = loss_criterion(predictions, targets)
# update weight(SGD)
optimizer.zero_grad()
loss.backward() # gradient 계산
optimizer.step() # update weight
# Check accuracy on training & test to see how good our model
train_accuracy, train_loss = check_accuracy(train_loader, model, loss_criterion)
train_accuracy_list.append(train_accuracy)
train_loss_list.append(train_loss)
test_accuracy, test_loss = check_accuracy(test_loader, model, loss_criterion)
test_accuracy_list.append(test_accuracy)
test_loss_list.append(test_loss)
print(f'epoch = {epoch} : train_loss = {train_loss:.4f}, test_loss = {test_loss:.4f},')
# accuracy/loss graph
draw_graph(train_accuracy_list, train_loss_list, test_accuracy_list, test_loss_list)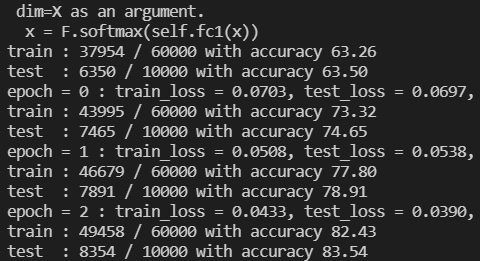
출력 결과를 보면 에폭0(epoch)일때는 학습 정확도가 63.26%밖에 되지 않지만 점점 학습을 하면서 최종적으론 86.88%의 정확도를 보이는 것을 알 수 있다. 86%도 나름 높은 확률이지만 이런 수치로 서비스를 구현하기엔 정확도가 많이 부족하다.
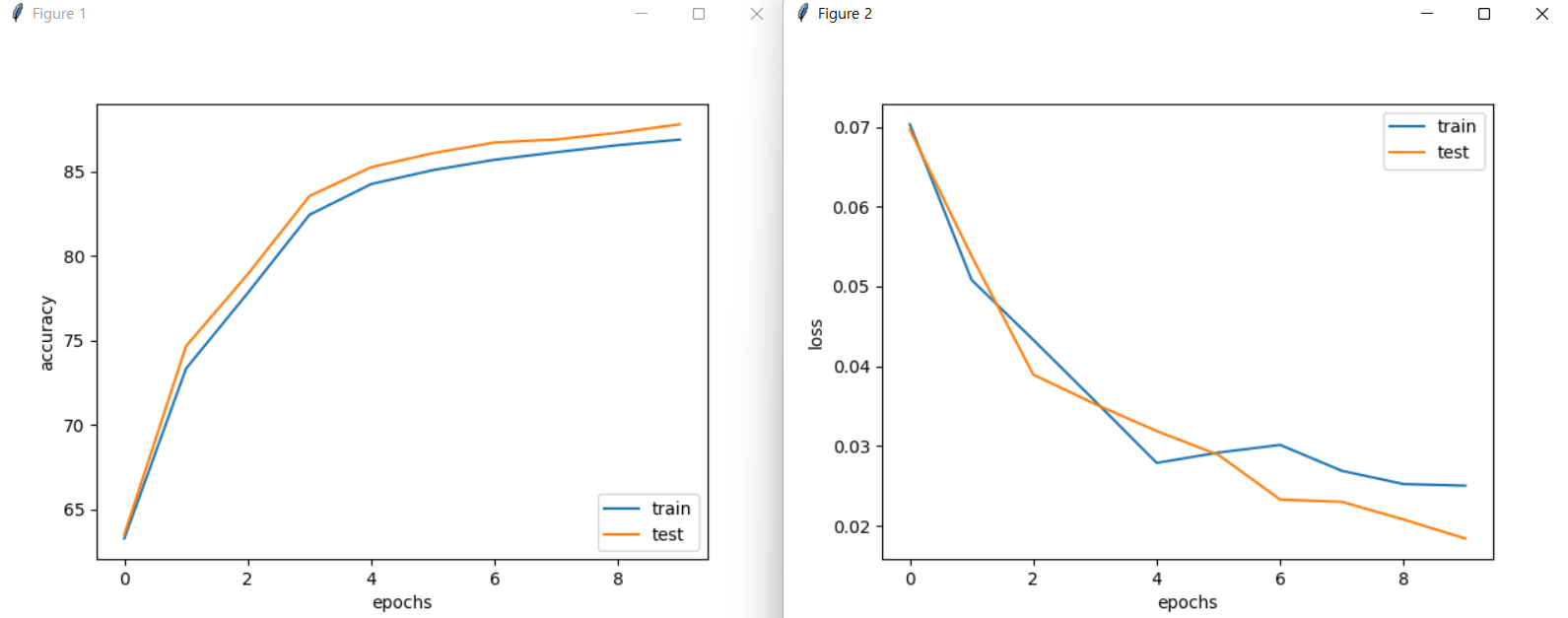
그래프도 함께 확인해보면 정확도는 증가하고 오차도 줄어드는 것을 확인할 수 있다.
이것만 보면 꽤 괜찮은 수치인 것 같지만 오늘날 사용하는 다른 알고리즘과 비교하면 한참 못미치는 수치이다.
다음엔 이보다 더 높은 정확도와 학습을 더 빨리 할 수 있도록 하는 cross-entropy를 이용한 모델을 다뤄보자.